CMU10714 dlsys lec14 卷积的实现

本节介绍了卷积的不同实现方法。

存储结构

首先需要明确tensor在内存中是如何存储的。我们假设被卷积的图像高度为\(H\)，宽度为\(W\)，通道数为\(C_{in}\)，卷积核的大小为\(K\times K\)，卷积的输出通道数为\(C_{out}\)。同时还有批量维度，\(N\)。

图像的表示方法为float Z[N][H][W][C_in]，这种表示方法称为NHWC格式，pytorch中的存储格式是NCHW，只考虑每张图片计算速度，我们的这种表示更好，但对大批量卷积pytorch的格式友好。

卷积核的表示方法为float W[K][K][C_in][C_out]。可以将卷积核视为\(K\times K\) 个 \(C_{in}\times C_{out}\)矩阵的矩阵（其实本来就是这样）。注意pytorch其实使用了[C_out][C_in][K][K]的格式。

Baseline

首先写一个参考答案，直接使用Pytorch实现，目的是检查我们代码的正确性，以及比较时间。

import torch
import torch.nn as nn
import numpy as np

def conv_reference(Z, weight):
    # NHWC -> NCHW
    z_torch = torch.tensor(Z).permute(0, 3, 1, 2)
    # KKIO -> OIKK
    W_torch = torch.tensor(weight).permute(3, 2, 0, 1)
    out = nn.functional.conv2d(z_torch, W_torch)
    return out.permute(0, 2, 3, 1).contiguous().numpy()

Z = np.random.randn(10, 32, 32, 8)
W = np.random.randn(3, 3, 8, 16)

暴力循环

最简单的实现卷积的方法就是直接嵌套for循环了。

def conv_naive(Z, weight):
    N, H, W, C_in = Z.shape
    K, _, _, C_out = weight.shape

    out = np.zeros((N, H-K+1, W-K+1, C_out))
    for n in range(N):
        for c_in in range(C_in):
            for c_out in range(C_out):
                for y in range(H-K+1):
                    for x in range(W-K+1):
                        for i in range(K):
                            for j in range(K):
                                out[n, y, x, c_out] += Z[n, y+i, x+j, c_in] * weight[i, j, c_in, c_out]
    return out

但对于Z为(10, 32, 32, 8)，W为(3, 3, 8, 16)。

暴力循环的时间：

Pytorch的时间：

。。。

使用矩阵乘法

首先设想卷积核大小为\(1\times 1\)的时候，卷积操作就是矩阵乘法：将图片每个位置的长为\(C_{in}\)的向量，乘以大小为\(C_{in}\times C_{out}\)的矩阵。

如

Z = np.random.randn(10, 32, 32, 8)
W1 = np.random.randn(1, 1, 8, 16)
out2 = Z @ W1
print(np.linalg.norm(out-out2))
---
1.0738548044478649e-14

于是推广到\(K\times K\)的卷积核，实际上是卷积核“中”每个“矩阵”与原始图像对应位置的那些向量做矩阵乘法，然后将得到的向量相加。

于是可以这么实现：

def conv_matrix_mul(Z, weight):
    N, H, W, C_in = Z.shape
    K, _, _, C_out = weight.shape

    out = np.zeros((N, H-K+1, W-K+1, C_out))
    for i in range(K):
        for j in range(K): # 迭代卷积核的每个位置
            out += Z[:, i:i+H-K+1, j:j+W-K+1, :] @ weight[i, j] # 将图像上的向量与卷积核的特定矩阵做乘法的结果加到对应的位置上
    return out

这个实现方法用时为：

还是比Pytorch要慢

使用im2col实现卷积

另一种矩阵乘法的视角

回顾上一节课，考虑简单的1D卷积，输入维度为5，padding为1，卷积核大小为3时，有 \[ \begin{bmatrix} 0& x_1& x_2 & x_3 & x_4 & x_5 &0\end{bmatrix} * \begin{bmatrix} w_1& w_2& w_3\end{bmatrix}=\begin{bmatrix} z_1& z_2 & z_3 & z_4 & z_5\end{bmatrix} \] 可以写成两个矩阵相乘的形式： \[ \begin{bmatrix}z_1 \\z_2 \\z_3 \\z_4 \\z_5\end{bmatrix}=\begin{bmatrix} 0 & x_1 & x_2\\ x_1 & x_2 &x_3 \\ x_2 & x_3 & x_4\\ x_3 & x_4 & x_5\\ x_4 & x_5 & 0 \end{bmatrix} \times \begin{bmatrix}w_1 \\w_2 \\ w_3\end{bmatrix} \] 虽然这样做看起来很浪费空间，但现实中大家都是这么实现的（。

而且这么表示卷积，可以方便地进行求导，解释一下，不想看的可以直接看下一节：

令\(z=conv(x, W)\)，我们要计算partial adjoints: \(\bar{v}\frac{\partial z}{\partial W}\)和\(\bar{v}\frac{\partial z}{\partial x}\)，因为\(\bar{v}\)已经在反向过程中已知了，所以就是要求\(\frac{\partial z}{\partial W}\)和\(\frac{\partial z}{\partial x}\)。

首先有一个简单的问题，对于\(x\in \R^n, W\in \R^{m\times n},z=Wx\) ，则\(\frac{\partial z}{\partial x}=W\)，则x的partial adjoint为\(W^T\bar{v}\)，即反向时候只需要计算W的转置即可。

我们发现卷积可以写成上面的矩阵与向量相乘的形式，于是我们可以知道 \[ \frac{\partial z}{\partial w} =\begin{bmatrix} 0 & x_1 & x_2\\ x_1 & x_2 &x_3 \\ x_2 & x_3 & x_4\\ x_3 & x_4 & x_5\\ x_4 & x_5 & 0 \end{bmatrix}^T \] on the other hand，卷积也可以写成 \[ \begin{bmatrix}z_1 \\z_2 \\z_3 \\z_4 \\z_5\end{bmatrix}=\begin{bmatrix} w_2 & w_3 & 0&0&0\\ w_1 & w_2 & w_3&0&0 \\ 0&w_1 & w_2 & w_3&0\\ 0&0&w_1 & w_2 & w_3\\ 0&0&0&w_1 & w_2 \end{bmatrix} \times \begin{bmatrix}x_1 \\x_2 \\ x_3 \\ x_4\\x_5\end{bmatrix} \] 于是 \[ \frac{\partial z}{\partial x} =\begin{bmatrix} w_2 & w_3 & 0&0&0\\ w_1 & w_2 & w_3&0&0 \\ 0&w_1 & w_2 & w_3&0\\ 0&0&w_1 & w_2 & w_3\\ 0&0&0&w_1 & w_2 \end{bmatrix}^T = \begin{bmatrix} w_2 & w_1 & 0&0&0\\ w_3 & w_2 & w_1&0&0 \\ 0&w_3 & w_2 & w_1&0\\ 0&0&w_3 & w_2 & w_1\\ 0&0&0&w_3 & w_2 \end{bmatrix} \] 而\(\bar{v}\frac{\partial z}{\partial x}\) 其实就是对\(\bar{v}\)用转置卷积核\(w_{flipped}\) （\([w_3,w_2,w_1]\)）卷积！

神奇函数：as_strided

通常情况下，一个\(M\times N\)的矩阵在底层是以row major方法以一维的形式存储的，即一行一行存储，扩展到多维的数组\(A\times B\times C\)，则是按照由后向前的order存储。通过strides的方法来获取多维的元素。如在float A[M][N]中，它的stride为\((N, 1)\)，如果我们想获取\(A[3][2]\)，则是获取一维数组的第\(3 \times N + 2\)个元素。

进一步的，我们想更好利用CPU的缓存机制，方便向量化的操作，我们要把矩阵分为TILE x TILE的小块（如TILE=4）

1	float A[M/TILE][n/TILE][TILE][TILE]

我们就可以在小块上进行高效操作，因为A的TILE x TILE的块在内存中是连续排布的。

如将一个6 x 6的矩阵

划分为TILE=2的小块，结果应该是这样：

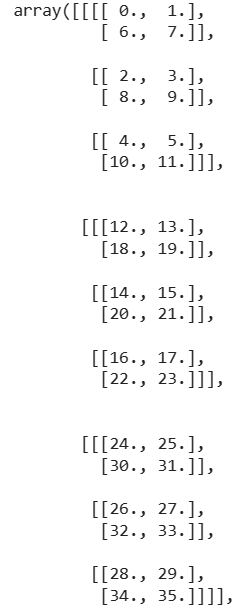
我们需要使用numpy中一个非常神奇的函数：np.lib.stride_tricks.as_strided()来实现。

这个函数可以让我们指定数组的shape和strides，但不修改底层数据，最终我们只需要用np.ascontiguousarray()来使内存连续排布即可。

首先看一下我们目的的矩阵大小是什么，我们选取了TILE=2，所以最终的shape应该是\(3\times 3\times 2 \times 2\)。

接下来我们看一下strides是多少，strides需要与shape相同，对于第一维，我们每次增加都想下降两行，如现在我们指在1，那么第一维加1后，我们应该指在13，所以第一维的stride为12；而第二维，每次增加1都想向左移两位，所以第二维的stride为2；第三维每次增加1都想下降一行，所以第三维stride为6；对于最后一位，每增加1只向右移动1个即可，所以stride=1，

于是我们可以构造矩阵B

1 2	from numpy.lib.stride_tricks import as_strided B = as_strided(A, shape=(3, 3, 2, 2), strides=np.array((12, 2, 6, 1))4) # 4是因为strides的单位是Byte

然后将B重新排列

1	C = np.ascontiguousarray(B)

就得到了内存紧凑我们想要的数组。

使用im2col实现卷积

首先看输出通道为1的二维卷积核在通道数为1的二维图片上做卷积的操作，

1 2	A = np.arange(36, dtype=np.float32).reshape(6, 6) W = np.arange(9, dtype=np.float32).reshape(3, 3)

我们按照上面的做法，将原始形状为\([6][6]\)的A变化成为\([2][2][3][3]\)的矩阵：

1	B = np.lib.stride_trices.as_strided(A, shape=(4, 4, 3, 3), strides=4 * (np.array((6, 1, 6, 1))))

然后把B拍平，与同样拍平的W做乘法，再reshape到正常大小：

1	(B.reshape(16, 9) @ W.reshape(9)).reshape(4, 4)

这样就可以实现卷积了！

但注意reshape的操作隐式的调用了ascontinugousarray，也就意味着我们并不能节省内存的开销，该开的还是得开。

按照以上思想，可以实现卷积如下：

def conv_im2col(Z, weight):
    N, H, W, C_in = Z.shape
    K, _, _, C_out = weight.shape
    Ns, Hs, Ws, Cs = Z.strides
    
    inner_dim = K * K * C_in
    A = as_strided(Z, shape=(N, H-K+1, W-K+1, K, K, C_in),
                   strides=(Ns, Hs, Ws, Hs, Ws, Cs)).reshape(-1, inner_dim)
    out = A @ weight.reshape(-1, C_out)
    return out.reshape(N, H-K+1, W-K+1, C_out)

这样用时为