[论文阅读] Transferable Sparse Adversarial Attack

CVPR2022 可迁移的稀疏对抗攻击

题目：Transferable Sparse Adversarial Attack

作者：Ziwen He

会议：CVPR2022

摘要翻译

深度神经网络已经表现出对对抗攻击的脆弱性。在本文中，我们聚焦于基于l0范数的稀疏对抗攻击，只用次改几个像素即可攻击成功。先前的稀疏攻击方法尽管有高攻击成功率，但在黑盒设置下，由于对代理模型的过拟合，对抗样本具有较低的迁移性。因此，我们提出了一个生成器架构去减轻过拟合问题，并且有效地生成可迁移的稀疏对抗样本。特别的，我们提出的生成器将稀疏扰动解耦为振幅和位置分量。我们精心设计了一个随机量化算子，以用端到端的方法联合优化这两个分量。实验表明我们的方法在相似的系数性设置下，相比于SOTA已经大大提升了迁移性。除此之外，我们的方法也实现了优越的推理速度，比其他基于优化的方法快了700倍。代码已公开。

基本问题

论文解决的问题： 基于L0范数的稀疏对抗攻击
动机：
1. 现有的稀疏对抗方法如PGD0, SparseFool, GreedyFool依赖于目标模型的梯度或其估计，具有较低的迁移性。并且有研究表明$l_2$和$l_\infin$范数限制的攻击在不同架构模型下更具有迁移性，$l_0$范数限制的稀疏对抗样本的迁移性还未知。
2. 之前的生成式方法都只生成稠密扰动，本文工作与之前生成式方法最大的不同就是有稀疏性的限制。
贡献：
- 探索稀疏对抗样本迁移性问题，并提出一个生成可迁移的稀疏对抗样本的方法。

Method

Analysis

对于无目标攻击，要优化的问题是：

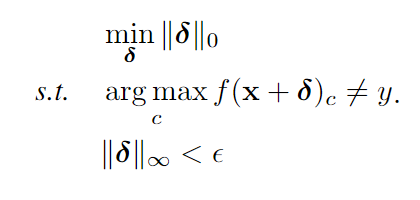
其中 $\epsilon$ 是$l_\infty$的扰动限制，如果是有目标攻击，则第二行要换为$arg\,max_c\,\,F(x_{adv})_c=y_t$， $f(x)_c$ 是类别c的logit值，目标类别是$y_t$ 。

之前的稀疏攻击方法很大的依赖于单个图像的梯度，而基于生成的方法，生成器可以学到自然图像到稀疏对抗图像的映射，生成器的参数是由数据分布学习到的，而不是单个图像。大量的训练数据可以减轻过拟合，增加迁移性。

（这里提出了用生成式的方法提升稀疏样本的迁移性，于是以下该探索如何设计一个生成器架构）。

但是优化上式是一个Np hard的问题，先前的工作是优化近似的$l_1$约束问题，如SparseFool，但其方法中包含了不可微分的步骤，于是不能进行端到端训练。

要解决这个$l_1$约束问题最直接的方法就是加一个$l_1$正则化项，但是这样做会使生成的扰动收敛于0，生成稠密扰动，如果直接在这个稠密扰动上面使用二值化（即选某些点保留扰动，其余不扰动），则会丢失信息而导致样本不再有攻击性。本文使用将扰动分解为幅度和位置两个变量的哈达玛乘积来解决这个问题，即$\delta =r \odot m$，其中$r\in R^N$，是扰动大小，$m\in \{0,1\}^N$，是表示此位置是否施加扰动。同时优化这两个向量，并且只给向量 $m$ 添加 $l_1$ 正则，即可实现稀疏的目标。

Framework

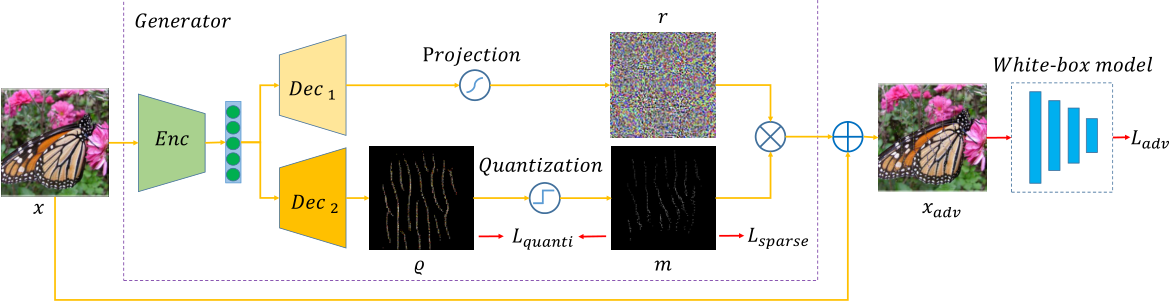
如上图，实现了两个分支分别生成 $r$ 和 $m$。

记编码器为$E$，则编码器生成的latent code $z = E(x)$，之后 $z $ 将被送入$D_1,D_2$两个解码器。

$D_1$ 生成对抗扰动的大小，结果 $r$ 将$D_1(z)$ 缩放到$[-255, 255]$ 之间。

$D_2$ 生成向量$Q\in [0,1]^N$，为得到离散的向量 $m$，使用一个二值化算子 $q$

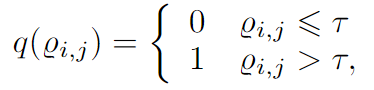
但显然这个函数的梯度都是0，会导致$D_2$的参数无法更新，于是本文设计了一个随机算子，随机变量$X\in \{0, 1\}$，如果$X=1$，则$Q_{i,j}$被量化为0,1，否则$q_{i,j}=Q_{i,j}$。其中$X$服从参数为p的伯努利分布，p为$X=1$的概率。

其实就是，如果$X=1$，则$Q$被量化，阻断反向传播；如果$X=0$，则$Q$保持原状，允许梯度传递，从而可以更改$D_2$的参数。

在推理过程中， p设置为1。

Loss functions

Adversial loss

这里使用C&W的loss

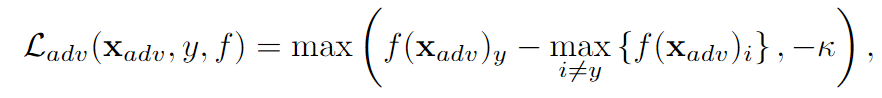
如果是有目标攻击的话，使用

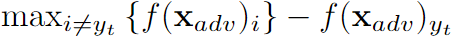
代替第一项。

Sparse loss

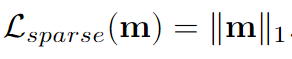
本方法的稀疏度主要是由 $m$ 决定的，由于$L_0$很难优化求解，于是使用$L_1$代替（L1范数是L0范数的最优凸近似，且L1范数容易优化求解），相应的，在下面的loss中，我们要让$m$中的值尽量趋近于0或者1。

Quantization loss

为减小训练和测试之间的gap，在损失函数中增加一项，使得Qij的值趋近于0或1

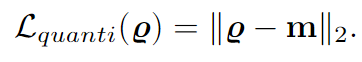
总体loss为

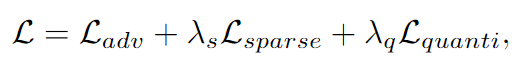
实验

大致进行了四个实验。

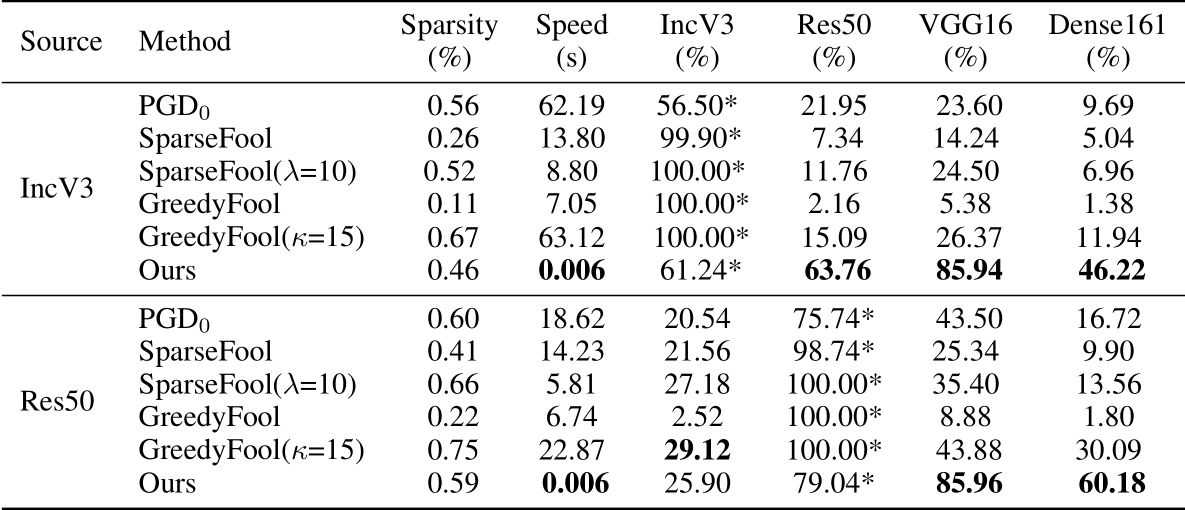
在类似的稀疏约束条件下，在不同的$l_\infty$条件下，测试与另外三个稀疏对抗攻击算法的Non-target的性能。
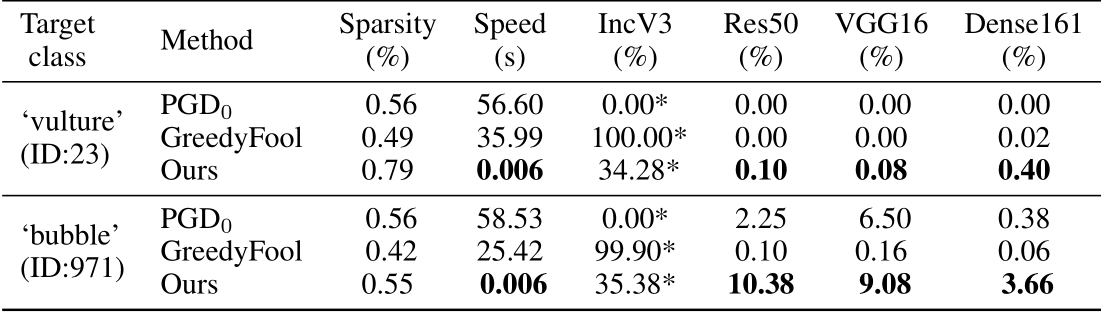
在类似的稀疏约束条件下，测试与另外两个稀疏对抗攻击算法在Target设定下的性能。但目标类别只有两个，“秃鹫”和“泡泡”。
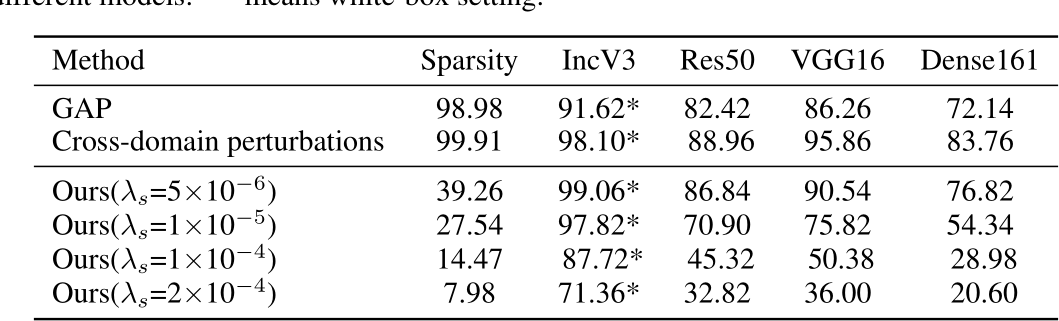
与GAP和Cross-domain perturbations在Non-target设定下进行相似评估。
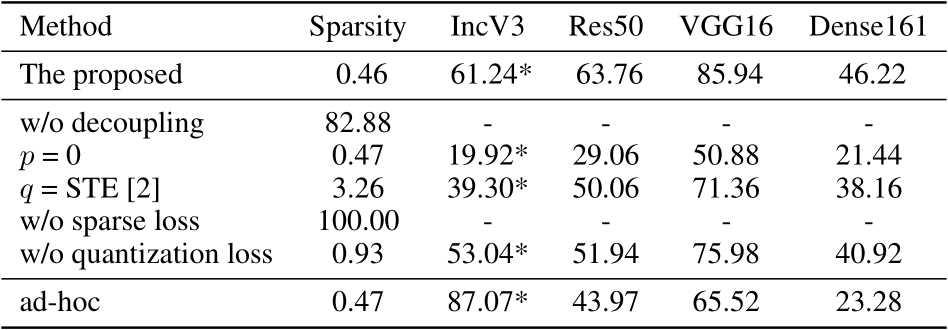
消融实验：（1）不解耦为幅度和位置分量的性能；（2）训练时使p=0时（即不进行量化）的性能，q=STE的性能；（3）不使用稀疏性约束loss（即不要L0约束）的性能；（4）不使用量化损失的性能；（5）对于每张图片训练自己的生成器的性能。

实验结果描述为：

相比于其他三个类似的方法，这个方法在Non-target下的迁移性大大提升，（白盒下效果反而不好，这是由于使用训练好的生成器做的原因，不过不重要）
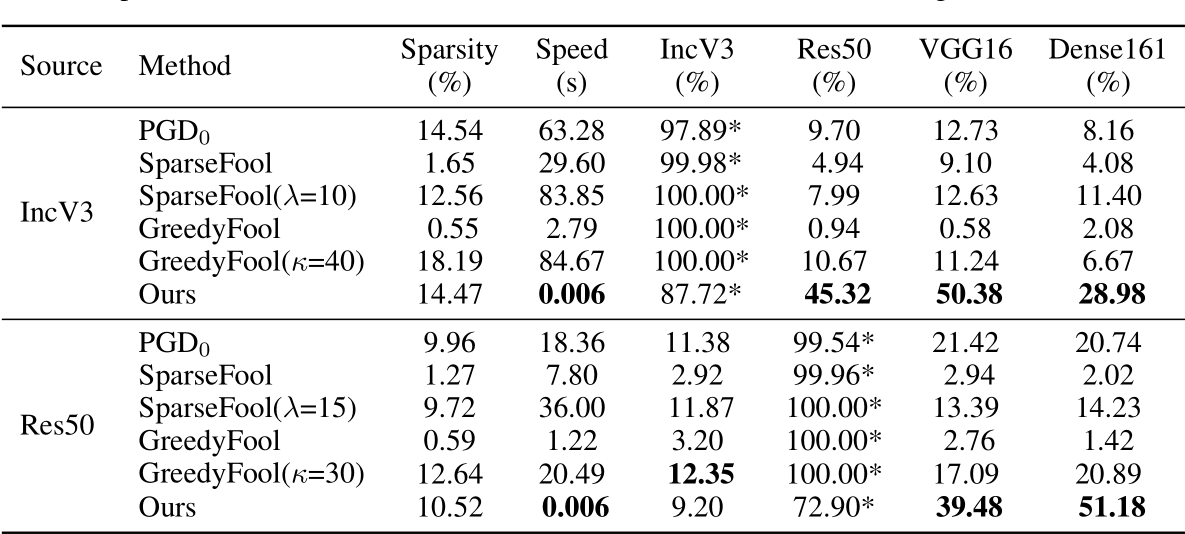
相比于其他两个类似的方法，这个方法在Target设定下也有一定的迁移效果，其他两种方法迁移性很差。随有提升，但貌似也不高。在实验中只进行了两个target class的实验，迁移性差别明显，可能是未来研究的一个方向。
相比于其他的基于生成的方法，发现在进行更少的扰动的情况下，也能达到甚至超过稠密扰动的生成式方法，这表明有很多扰动是无用的，甚至有负优化。
（1）去掉解耦，发现不能真正的实现稀疏。

（2）去掉量化，即使训练中的p=0，发现仍能实现稀疏，但是生成的对抗样本迁移性下降。并且与STE方法比较，发现结果比STE方法好。

（3）去掉sparse loss，生成的对抗样本变为100%的dense attack。

（4）去掉quantization loss，稀疏程度提高了（更改像素变多），并且迁移性降低了，验证了量化操作带来的信息损失会影响测试时的性能。

（5）使用每张图片生成自己的生成器的方法，发现白盒攻击效果提高了，但是黑盒攻击迁移性降低了，证明使用大量数据进行训练可以减小过拟合并提高迁移性的假设是正确的。

结论

本文提出了一种基于生成器的稀疏对抗攻击框架。在相同的稀疏性条件下，该方法比现有的现有方法具有更强的可迁移性，推理速度更快。根据经验，我们观察到，当对大规模ImageNet攻击时，我们的方法产生最先进的结果。我们的工作阐明了可转移的基于$l_0$的稀疏对抗样本的存在，并说明了最先进的白盒稀疏攻击方法倾向于找到修改像素数量最少但不具有迁移性的对抗样本。这两种类型的稀疏对抗攻击对于分析dnn的漏洞和评估安全风险(如在物理世界中创建可转移的对抗补丁来欺骗自动驾驶汽车)同样重要。

思考

方法的局限或问题：

用的损失函数是C&W的loss，与人脸识别中通常使用的特征图的余弦值或L2dis不同。
直觉上觉得，这个方法只适用于黑盒模型训练数据已知的情况。①如果黑盒模型训练数据未知（这里想强调的是类别不知道），则无法使用C&W loss，无法使用logits。②如果训练数据未知，那么学出的样本到对抗样本之间的映射，是不是有domain shift。

几个想法：

在训练数据未知的情况下。如果使用大量数据进行预训练，并且在单张图片上进行fine tune的效果如何？
如何将这个方法迁移到人脸识别系统的攻击上。这个方法是否与对抗补丁有联系。
提出的随机化量化方法很有趣，模型性能与p的关系是什么呢。当Q被量化为0,1时，阻断反向传播，这时Dec2参数不更新，并按照测试条件更新Dec1参数；当Q不被量化时，允许梯度的传递，这时Dec2参数进行更新（既有让结果趋近0或1，也有生成效果更好的对抗样本），同时Dec1也在更新参数，只不过设定是训练条件下。